In the previous post we discussed lighting and environment mapping, and our evaluation of the lighting contribution was performed in view space. Here we will discuss lighting in tangent space and extend our lighting model to include a normal map. If we apply a texture to a surface, then for every point in the texture we can define a set of vectors that are tangent to that point. Once we transform our light vector, halfway vector, and normal vector into tangent space, we can use the normal map to perturb our normal vector giving us the illusion of depth. Below are two screen captures of the result. The first has normal mapping enabled. In the second normal mapping has been disabled.


Below is a repeating stone texture we will use as our base texture (available here).

Below we have used the normalmap plugin for GIMP to generate our normal map texture. This texture has vector information encoded as red, green, and blue color values. When we we access this texture in our fragment shader, the red, green, and blue values will be in the range \([0.0,1.0]\). We'll need to transform these values to the range \([-1.0,1.0]\) using the following equation:
\begin{align}
\vec{n} &= 2 \cdot [\vec{c} - (0.5, 0.5, 0.5)]\\
\end{align}

Before we get into the gritty details, below is a video capture of the result.
In tangent space we have three basis vectors, \(\vec{T}\), the tangent vector, \(\vec{B}\), the bitangent vector, and \(\vec{N}\), the normal vector. In the diagram below we have the points, \(\vec{p}_0\), \(\vec{p}_1\), and \(\vec{p}_2\), and the vectors, \(\vec{v}_1\) and \(\vec{v}_2\), defined in object space. The points, \(\vec{t}_0\), \(\vec{t}_1\), and \(\vec{t}_2\), and the vectors, \(\vec{u}_1\) and \(\vec{u}_2\), are defined in tangent space. We seek the transformation matrix the takes as input a vector in tangent space, \(\vec{u}_3\), and yields a vector in object space, \(\vec{v}_3\). Ultimately, we'll want to take a vector in object space and transform it to tangent space, so we'll use the inverse of the transformation matrix. We have the following,
\begin{align}
\begin{bmatrix} v_{1,x} & v_{2,x} \\ v_{1,y} & v_{2,y} \\ v_{1,z} & v_{2,z} \end{bmatrix} &= \begin{bmatrix} T_x & B_x \\ T_y & B_y \\ T_z & B_z \end{bmatrix} \begin{bmatrix} u_{1,x} & u_{2,x} \\ u_{1,y} & u_{2,y} \end{bmatrix}\\
\begin{bmatrix} v_{1,x} & v_{2,x} \\ v_{1,y} & v_{2,y} \\ v_{1,z} & v_{2,z} \end{bmatrix} \begin{bmatrix} u_{1,x} & u_{2,x} \\ u_{1,y} & u_{2,y} \end{bmatrix}^{-1} &= \begin{bmatrix} T_x & B_x \\ T_y & B_y \\ T_z & B_z \end{bmatrix}\\
\begin{bmatrix} v_{1,x} & v_{2,x} \\ v_{1,y} & v_{2,y} \\ v_{1,z} & v_{2,z} \end{bmatrix} \begin{bmatrix} u_{2,y} & -u_{2,x} \\ -u_{1,y} & u_{1,x} \end{bmatrix}\frac{1}{u_{1,x}u_{2,y}-u_{2,x}u_{1,y}} &= \begin{bmatrix} T_x & B_x \\ T_y & B_y \\ T_z & B_z \end{bmatrix}\\
\end{align}
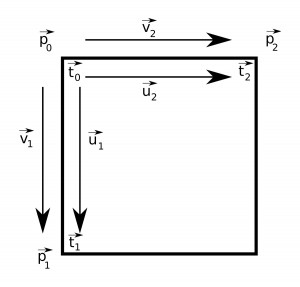
We now have the vectors, \(\vec{T}\) and \(\vec{B}\), and we can find the normal vector by crossing the bitangent with the tangent (if the vertical axis in our texture space were increasing upward, we would cross the tangent with the bitangent to ensure our normal is pointing in the right direction).
\begin{align}
\vec{N} &= \vec{B} \times \vec{T}\\
\end{align}
Thus, we have the matrix, \(\mathbf{M}\), that maps vectors in tangent space to vectors in object space. The inverse will allow us to map from object space to tangent space.
\begin{align}
\mathbf{M} &= \begin{bmatrix} T_x & B_x & N_x \\ T_y & B_y & N_y \\ T_z & B_z & N_z \end{bmatrix}\\
\end{align}
In our code we will define a structure to contain the vertex, the normal vector, the texture coordinate, and the \(\vec{T}\), \(\vec{B}\), and \(\vec{N}\) vectors.
struct vertex_ {
GLfloat x, y, z;
GLfloat nx, ny, nz;
GLfloat tx, ty, tz;
GLfloat _tx, _ty, _tz;
GLfloat _bx, _by, _bz;
GLfloat _nx, _ny, _nz;
GLfloat padding[14];
};
Once we have defined our vertices, we can use the following function to compute the tangent space matrix based on the derivation above.
void computeTangentSpaceMatrix(vertex_& p0, const vertex_& p1, const vertex_& p2) {
GLfloat v1x, v1y, v1z, v2x, v2y, v2z, u1x, u1y, u2x, u2y, det;
v1x = p1.x - p0.x;
v1y = p1.y - p0.y;
v1z = p1.z - p0.z;
v2x = p2.x - p0.x;
v2y = p2.y - p0.y;
v2z = p2.z - p0.z;
u1x = p1.tx - p0.tx;
u1y = p1.ty - p0.ty;
u2x = p2.tx - p0.tx;
u2y = p2.ty - p0.ty;
det = u1x * u2y - u2x * u1y;
p0._tx = (v1x * u2y - v2x * u1y) / det;
p0._ty = (v1y * u2y - v2y * u1y) / det;
p0._tz = (v1z * u2y - v2z * u1y) / det;
p0._bx = (-v1x * u2x + v2x * u1x) / det;
p0._by = (-v1y * u2x + v2y * u1x) / det;
p0._bz = (-v1z * u2x + v2z * u1x) / det;
p0._nx = p0._by * p0._tz - p0._bz * p0._ty;
p0._ny = p0._bz * p0._tx - p0._bx * p0._tz;
p0._nz = p0._bx * p0._ty - p0._by * p0._tx;
}
Below we define a cube, evaluate the tangent space matrix for each vertex, and set up our vertex buffer objects.
vertex_ vertices[] = {
{-1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0},
{-1.0, -1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 1.0, 0.0},
{ 1.0, -1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0},
{ 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 0.0, 0.0},
{ 1.0, 1.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, 0.0},
{ 1.0, -1.0, -1.0, 0.0, 0.0, -1.0, 0.0, 1.0, 0.0},
{-1.0, -1.0, -1.0, 0.0, 0.0, -1.0, 1.0, 1.0, 0.0},
{-1.0, 1.0, -1.0, 0.0, 0.0, -1.0, 1.0, 0.0, 0.0},
{ 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0},
{ 1.0, -1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 1.0, 0.0},
{ 1.0, -1.0, -1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 0.0},
{ 1.0, 1.0, -1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0},
{-1.0, 1.0, -1.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0},
{-1.0, -1.0, -1.0, -1.0, 0.0, 0.0, 0.0, 1.0, 0.0},
{-1.0, -1.0, 1.0, -1.0, 0.0, 0.0, 1.0, 1.0, 0.0},
{-1.0, 1.0, 1.0, -1.0, 0.0, 0.0, 1.0, 0.0, 0.0},
};
computeTangentSpaceMatrix(vertices[0], vertices[1], vertices[2]);
computeTangentSpaceMatrix(vertices[1], vertices[2], vertices[3]);
computeTangentSpaceMatrix(vertices[2], vertices[3], vertices[0]);
computeTangentSpaceMatrix(vertices[3], vertices[0], vertices[1]);
computeTangentSpaceMatrix(vertices[4], vertices[5], vertices[6]);
computeTangentSpaceMatrix(vertices[5], vertices[6], vertices[7]);
computeTangentSpaceMatrix(vertices[6], vertices[7], vertices[4]);
computeTangentSpaceMatrix(vertices[7], vertices[4], vertices[5]);
computeTangentSpaceMatrix(vertices[8], vertices[9], vertices[10]);
computeTangentSpaceMatrix(vertices[9], vertices[10], vertices[11]);
computeTangentSpaceMatrix(vertices[10], vertices[11], vertices[8]);
computeTangentSpaceMatrix(vertices[11], vertices[8], vertices[9]);
computeTangentSpaceMatrix(vertices[12], vertices[13], vertices[14]);
computeTangentSpaceMatrix(vertices[13], vertices[14], vertices[15]);
computeTangentSpaceMatrix(vertices[14], vertices[15], vertices[12]);
computeTangentSpaceMatrix(vertices[15], vertices[12], vertices[13]);
unsigned int indices[] = {
0, 1, 2, 3,
4, 5, 6, 7,
8, 9, 10, 11,
12, 13, 14, 15,
};
GLuint vbo_vertices, vbo_indices;
glGenBuffers(1, &vbo_vertices);
glBindBuffer(GL_ARRAY_BUFFER, vbo_vertices);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
glGenBuffers(1, &vbo_indices);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, vbo_indices);
glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);
In the code below we load our texture and normal map, set up our shader, and retrieve our attribute and uniform locations.
GLuint texture2;
SDL_Surface *tex2 = IMG_Load("media/texture_4.png");
setupTexture(texture2, tex2);
SDL_FreeSurface(tex2);
GLuint texture2normal;
SDL_Surface *tex2nor = IMG_Load("media/normal_4.png");
setupTexture(texture2normal, tex2nor);
SDL_FreeSurface(tex2nor);
GLuint glProgram2, glShaderV2, glShaderF2;
createProgram(glProgram2, glShaderV2, glShaderF2, "src/vertex2.sh", "src/fragment2.sh");
GLint vertex2 = glGetAttribLocation(glProgram2, "vertex");
GLint normal2 = glGetAttribLocation(glProgram2, "normal");
GLint texcoord2 = glGetAttribLocation(glProgram2, "texcoord");
GLint _tangent2 = glGetAttribLocation(glProgram2, "_tangent");
GLint _bitangent2 = glGetAttribLocation(glProgram2, "_bitangent");
GLint _normal2 = glGetAttribLocation(glProgram2, "_normal");
GLint texture_sample2 = glGetUniformLocation(glProgram2, "texture_sample");
GLint normal_sample2 = glGetUniformLocation(glProgram2, "normal_sample");
GLint light_position2 = glGetUniformLocation(glProgram2, "light_position");
GLint Projection2 = glGetUniformLocation(glProgram2, "Projection");
GLint View2 = glGetUniformLocation(glProgram2, "View");
GLint Model2 = glGetUniformLocation(glProgram2, "Model");
GLint flag2 = glGetUniformLocation(glProgram2, "flag");
In order to render our cube we use the code below where the model, view, and projection matrices, in addition the light position have previously been defined. We must enable each attribute and declare the offset into our vertex_ structure for each attribute.
glUseProgram(glProgram2); glUniform3f(light_position2, light_position.x, light_position.y, light_position.z); glUniformMatrix4fv(Projection2, 1, GL_FALSE, glm::value_ptr(Projection)); glUniformMatrix4fv(View2, 1, GL_FALSE, glm::value_ptr(View)); glUniformMatrix4fv(Model2, 1, GL_FALSE, glm::value_ptr(Model)); glUniform1i(flag2, (int)normal); glUniform1i(texture_sample2, 0); glUniform1i(normal_sample2, 1); glActiveTexture(GL_TEXTURE0); glBindTexture(GL_TEXTURE_2D, texture2); glActiveTexture(GL_TEXTURE1); glBindTexture(GL_TEXTURE_2D, texture2normal); glBindBuffer(GL_ARRAY_BUFFER, vbo_vertices); glEnableVertexAttribArray(vertex2); glVertexAttribPointer(vertex2, 3, GL_FLOAT, GL_FALSE, sizeof(vertex_), 0); glEnableVertexAttribArray(normal2); glVertexAttribPointer(normal2, 3, GL_FLOAT, GL_FALSE, sizeof(vertex_), (char *)NULL + 12); glEnableVertexAttribArray(texcoord2); glVertexAttribPointer(texcoord2, 3, GL_FLOAT, GL_FALSE, sizeof(vertex_), (char *)NULL + 24); glEnableVertexAttribArray(_tangent2); glVertexAttribPointer(_tangent2, 3, GL_FLOAT, GL_FALSE, sizeof(vertex_), (char *)NULL + 36); glEnableVertexAttribArray(_bitangent2); glVertexAttribPointer(_bitangent2, 3, GL_FLOAT, GL_FALSE, sizeof(vertex_), (char *)NULL + 48); glEnableVertexAttribArray(_normal2); glVertexAttribPointer(_normal2, 3, GL_FLOAT, GL_FALSE, sizeof(vertex_), (char *)NULL + 60); glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, vbo_indices); glDrawElements(GL_QUADS, 16, GL_UNSIGNED_INT, 0);
The vertex shader below expects a vertex, normal vector, texture coordinate, tangent vector, bitangent vector, and normal vector, and yields a light vector, normal vector, and halfway vector in tangent space in addition to the texture coordinate. We first apply our model, view, and projection matrices to our vertex and then evaluate the inverse of our tangent space matrix. We then proceed to find our light vector, halfway vector, and normal vector in tangent space.
#version 330
in vec3 vertex;
in vec3 normal;
in vec3 texcoord;
in vec3 _tangent;
in vec3 _bitangent;
in vec3 _normal;
uniform vec3 light_position;
uniform mat4 Projection;
uniform mat4 View;
uniform mat4 Model;
out vec3 light_vector;
out vec3 normal_vector;
out vec3 halfway_vector;
out vec2 texture_coord;
void main() {
gl_Position = Projection * View * Model * vec4(vertex, 1.0);
mat3 tbni = inverse(mat3(_tangent, _bitangent, _normal));
vec4 v = Model * vec4(vertex, 1.0); // vertex in model space
light_vector = tbni * (inverse(Model) * vec4(light_position - v.xyz, 0)).xyz; // light vector in tangent space
v = View * Model * vec4(vertex, 1.0); // vertex in eye space
vec4 light_vector_eye = normalize((View * vec4(light_position, 1.0)) - v); // light vector in eye space
vec4 viewer_vector_eye = normalize(-v); // view vector in eye space
halfway_vector = tbni * (inverse(View * Model) * vec4((light_vector_eye.xyz + viewer_vector_eye.xyz), 0.0)).xyz;
// halfway vector in tangent space
normal_vector = inverse(transpose(tbni)) * normal;
texture_coord = texcoord.xy;
}
The fragment shader below is very similar to the fragment shader in the previous post. The main differences are the addition of a flag, to enable normal mapping, and a normal map used to perturb the normal vector.
#version 330
in vec3 normal_vector;
in vec3 light_vector;
in vec3 halfway_vector;
in vec2 texture_coord;
uniform sampler2D texture_sample;
uniform sampler2D normal_sample;
uniform bool flag;
out vec4 fragColor;
void main (void) {
vec3 normal1 = normalize(normal_vector);
vec3 light_vector1 = normalize(light_vector);
vec3 halfway_vector1 = normalize(halfway_vector);
vec4 c = texture(texture_sample, texture_coord);
vec3 n = normalize((texture(normal_sample, texture_coord).xyz-0.5)*2.0);
normal1 = flag ? normalize(n.xyz+normal1) : normal1;
vec4 emissive_color = vec4(0.0, 1.0, 0.0, 1.0); // green
vec4 ambient_color = vec4(1.0, 1.0, 1.0, 1.0); // white
vec4 diffuse_color = vec4(1.0, 1.0, 1.0, 1.0); // white
vec4 specular_color = vec4(1.0, 1.0, 1.0, 1.0); // white
float emissive_contribution = 0.01;
float ambient_contribution = 0.09;
float diffuse_contribution = 0.4;
float specular_contribution = 0.9;
float d = dot(normal1, light_vector1);
bool facing = d > 0.0;
fragColor = emissive_color * emissive_contribution +
ambient_color * ambient_contribution * c +
diffuse_color * diffuse_contribution * c * max(d, 0) +
(facing ?
specular_color * specular_contribution * c * pow(max(0,dot(normal1, halfway_vector1)), 200.0) :
vec4(0.0, 0.0, 0.0, 0.0));
fragColor.a = 1.0;
}
In this post we've derived the tangent space matrix and set up a shader program to enable normal mapping. If you have any questions or comments leave me a reply. Feel free to download this project. The code is a bit sloppy, but, hopefully, you can get it to function. It currently uses the joystick object from another post to navigate.
Download this project: normal.tar.bz2



Comments
Thank you so much for your computeTangentSpaceMatrix source, with a simple array vertex explanation. Really useful!