It's been a while since my last post. A project I have in the works requires some matrix decompositions, so I thought this would be a good opportunity to get a post out about QR decompositions using Householder transformations. For the moment we will focus on the field of real numbers, though we can extend these concepts to the complex field if necessary.
| Theorem. | A real matrix, \(\mathbf{A} \in \mathbf{M}_{m,n}\), can be decomposed as \(\mathbf{A}=\mathbf{Q}\mathbf{R}\), where \(\mathbf{Q} \in \mathbf{M}_{m,m}\) is an orthogonal matrix and \(\mathbf{R} \in \mathbf{M}_{m,n}\) is an upper triangular matrix. |
The proof of this theorem has been omitted but could be constructed using Householder transformations. We'll discuss the Householder transformation and see how it can be applied to perform the QR decomposition. We'll review the decomposition algorithm and, lastly, have a look at some C++ code.
A Householder transformation is a linear transformation given by the matrix, \(\mathbf{P}\),
\begin{align}
\mathbf{P} &= \mathbf{I} - 2\hat{v}\hat{v}^T\\
\end{align}
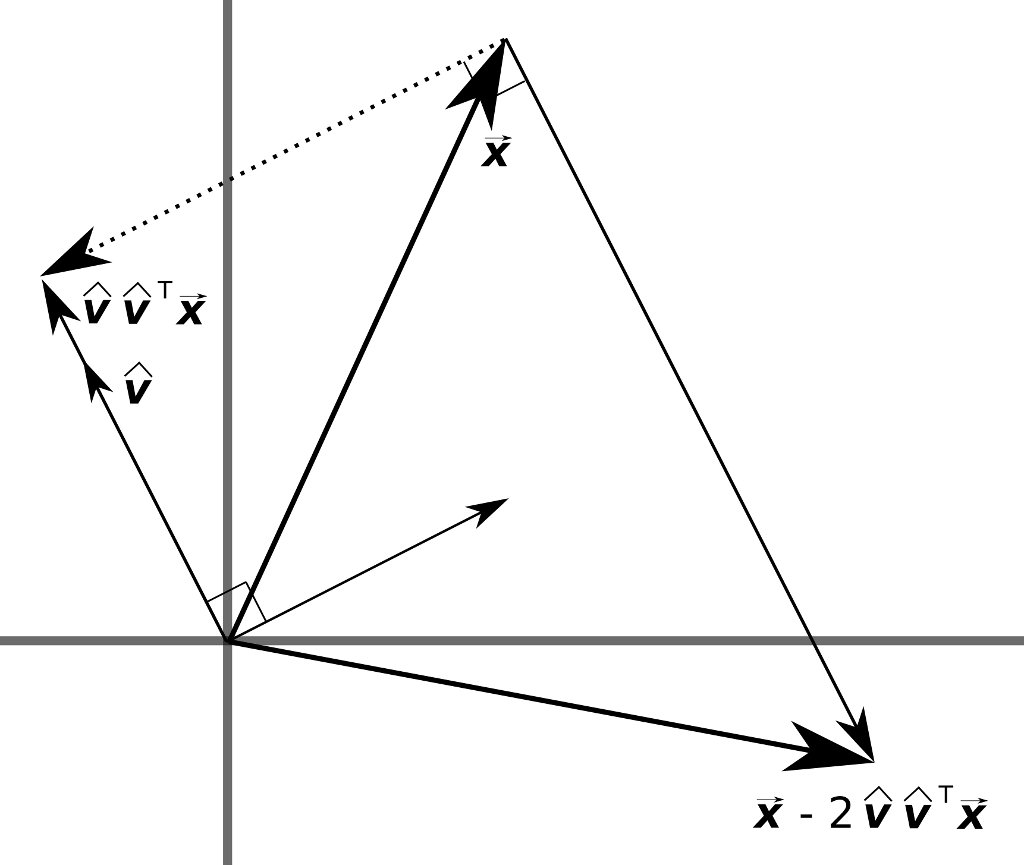
where \(\mathbf{I}\) is the identity matrix and \(\hat{v}\) is a unit vector. \(\mathbf{P}\vec{x}\) is the reflection of \(\vec{x}\) about the hyperplane passing through the origin with normal vector, \(\hat{v}\).
\begin{align}
\mathbf{P}\vec{x} &= \left(\mathbf{I} - 2\hat{v}\hat{v}^T\right)\vec{x}\\
&= \vec{x} - 2\hat{v}\hat{v}^T\vec{x}\\
\end{align}
If \(\hat{v}\hat{v}^T\vec{x}\) is the projection of \(\vec{x}\) onto \(\hat{v}\), then \(\mathbf{P}\vec{x}\) should reflect \(\vec{x}\) about the hyperplane with normal, \(\hat{v}\). See the diagram below.
Some properties of \(\mathbf{P}\) follow.
\begin{align}
\mathbf{P}^T &= \left(\mathbf{I} - 2\hat{v}\hat{v}^T\right)^T\\
&= \mathbf{I} - 2\left(\hat{v}\hat{v}^T\right)^T\\
&= \mathbf{I} - 2\hat{v}\hat{v}^T\\
&= \mathbf{P}
\end{align}
\(\mathbf{P}^T = \mathbf{P}\), thus, \(\mathbf{P}\) is symmetric.
\begin{align}
\mathbf{P}^T\mathbf{P} &= \mathbf{P}\mathbf{P}\\
&= \left(\mathbf{I} - 2\hat{v}\hat{v}^T\right)\left(\mathbf{I} - 2\hat{v}\hat{v}^T\right)\\
&= \mathbf{I} - 4\hat{v}\hat{v}^T + 4\hat{v}\hat{v}^T\hat{v}\hat{v}^T\\
&= \mathbf{I} - 4\hat{v}\hat{v}^T + 4\hat{v}\left(\hat{v}^T\hat{v}\right)\hat{v}^T\\
&= \mathbf{I} - 4\hat{v}\hat{v}^T + 4\hat{v}\hat{v}^T\\
&= \mathbf{I}
\end{align}
\(\mathbf{P}^T\mathbf{P} = \mathbf{I} \Leftrightarrow \mathbf{P}^T = \mathbf{P}^{-1}\), thus, \(\mathbf{P}\) is orthogonal.
\(\mathbf{P}^T\mathbf{P} = \mathbf{P}^2 = \mathbf{I}\), thus, \(\mathbf{P}\) is an involution.
Additionally,
\begin{align}
\mathbf{P}\vec{v} &= \left(\mathbf{I} - 2\hat{v}\hat{v}^T\right)\vec{v}\\
&= \vec{v} - 2\hat{v}\hat{v}^T\hat{v}\|\vec{v}\|\\
&= \vec{v} - 2\vec{v}\\
&= -\vec{v}\\
\end{align}
thus, \(-1\) is an eigenvalue of \(\mathbf{P}\) with multiplicity one.
For a vector, \(\vec{u}\), orthogonal to \(\vec{v}\), we have,
\begin{align}
\mathbf{P}\vec{u} &= \left(\mathbf{I} - 2\hat{v}\hat{v}^T\right)\vec{u}\\
&= \vec{u} - \vec{0}\\
&= \vec{u}\\
\end{align}
thus, \(1\) is an eigenvalue of \(\mathbf{P}\) with multiplicity \(m-1\), since there are \(m-1\) vectors orthogonal to \(\vec{v}\).
Now that we have touched on the Householder transformation, we'll see how the transformation can be applied to decompose a matrix into the product of an orthogonal matrix and an upper triangular matrix. The basic idea is to apply multiple transformations to successively zap the entries below the main diagonal column by column. We will then have something of the form,
\begin{align}
\mathbf{A} &= \left(\mathbf{Q}_1\mathbf{Q}_2\ldots\mathbf{Q}_n\right)\left(\mathbf{Q}_n\mathbf{Q}_{n-1}\ldots\mathbf{Q}_1\mathbf{A}\right)\\
\end{align}
Clearly, from the properties above, \(\mathbf{Q}_i\mathbf{Q}_i = \mathbf{I}\), so this is a valid statement. Additionally, \(\mathbf{Q}_1\mathbf{Q}_2\ldots\mathbf{Q}_n\) is the product of orthogonal matrices and is itself orthogonal. What is maybe not so clear at this point is that the product, \(\mathbf{Q}_n\mathbf{Q}_{n-1}\ldots\mathbf{Q}_1\mathbf{A}\), is an upper triangular matrix.
Consider \(\mathbf{A}\) as,
\begin{align}
\mathbf{A} &= \begin{pmatrix}
\vec{a_1} & \vec{a_2} & \cdots & \vec{a_n}\\
\end{pmatrix}\\
\end{align}
The first step is to find the Householder transformation, \(\mathbf{Q}_1 = \mathbf{I} - 2\hat{v_1}\hat{v_1}^T\), that rotates the vector, \(\vec{a_1}\), to the vector, \(\|\vec{a_1}\|\hat{e_1} = \begin{pmatrix}\|\vec{a_1}\| & 0 & \cdots & 0\end{pmatrix}^T\), which amounts to finding the appropriate unit vector, \(\hat{v_1}\). Note that we could also rotate the vector, \(\vec{a_1}\), to the vector, \(-\|\vec{a_1}\|\hat{e_1} = \begin{pmatrix}-\|\vec{a_1}\| & 0 & \cdots & 0\end{pmatrix}^T\). In our implementation we will choose the sign to improve numerical stability. For the vector, \(\vec{a_1}\), we will choose the sign to be \(-\text{sgn}(\hat{e_1}^T\vec{a_1})\).
If we choose \(\vec{v_1}\) such that,
\begin{align}
\vec{v_1} &= \frac{\vec{a_1}-\|\vec{a_1}\|\hat{e_1}}{\|\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\|}\\
\end{align}
where \(\hat{e_1}\) is a standard basis vector, then we can show that \(\mathbf{Q}_1\vec{a_1} = \|\vec{a_1}\|\hat{e_1}\) as follows. Working with the denominator,
\begin{align}
\mathbf{Q}_1\vec{a_1} &= \left[\mathbf{I} - 2\left(\frac{\vec{a_1}-\|\vec{a_1}\|\hat{e_1}}{\|\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\|}\right)\left(\frac{\vec{a_1}-\|\vec{a_1}\|\hat{e_1}}{\|\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\|}\right)^T\right]\vec{a_1}\\
&= \left[\mathbf{I} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T}{\left(\vec{a_1} - \|\vec{a_1}\|\hat{e_1}\right)^T\left(\vec{a_1} - \|\vec{a_1}\|\hat{e_1}\right)}\right]\vec{a_1}\\
&= \left[\mathbf{I} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T}{\left(\vec{a_1}^T - \|\vec{a_1}\|\hat{e_1}^T\right)\left(\vec{a_1} - \|\vec{a_1}\|\hat{e_1}\right)}\right]\vec{a_1}\\
&= \left[\mathbf{I} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T}{\vec{a_1}^T\vec{a_1} - 2\|\vec{a_1}\|\hat{e_1}^T\vec{a_1} + \|\vec{a_1}\|^2\hat{e_1}^T\hat{e_1}}\right]\vec{a_1}\\
&= \left[\mathbf{I} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T}{2\|\vec{a_1}\|^2 - 2\|\vec{a_1}\|\hat{e_1}^T\vec{a_1}}\right]\vec{a_1}\\
&= \left[\mathbf{I} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T}{2\left(\|\vec{a_1}\|^2-\|\vec{a_1}\|\hat{e_1}^T\vec{a_1}\right)}\right]\vec{a_1}\\
&= \left[\mathbf{I} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T}{2\left(\vec{a_1}^T\vec{a_1} - \|\vec{a_1}\|\hat{e_1}^T\vec{a_1}\right)}\right]\vec{a_1}\\
&= \left[\mathbf{I} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T}{2\left(\vec{a_1}^T - \|\vec{a_1}\|\hat{e_1}^T\right)\vec{a_1}}\right]\vec{a_1}\\
&= \left[\mathbf{I} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T}{2\|\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\|\vec{v_1}^T\vec{a_1}}\right]\vec{a_1}\\
\end{align}
Finishing up with the numerator,
\begin{align}
\mathbf{Q}_1\vec{a_1} &= \vec{a_1} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)^T\vec{a_1}}{2\|\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\|\vec{v_1}^T\vec{a_1}}\\
&= \vec{a_1} - 2\frac{\left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\|\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\|\vec{v_1}^T\vec{a_1}}{2\|\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\|\vec{v_1}^T\vec{a_1}}\\
&= \vec{a_1} - \left(\vec{a_1}-\|\vec{a_1}\|\hat{e_1}\right)\\
&= \|\vec{a_1}\|\hat{e_1}\\
\end{align}
Multiplying \(\mathbf{A}\\) by \(\mathbf{Q}_1\) yields a matrix of the following form.
\begin{align}
\mathbf{Q}_1\mathbf{A} &= \begin{pmatrix}\|\vec{a_1}\| & \star & \cdots & \star\\0 \\\vdots & & \mathbf{A_1}\\0\end{pmatrix}\\
\end{align}
Our job now is to find the matrix, \(\mathbf{Q}_2\), to deal with the sub-matrix \(\mathbf{A_1}\). Note that \(\mathbf{Q}_2\) will have the following form.
\begin{align}
\mathbf{Q}_2 &= \begin{pmatrix}
1 & 0 & \cdots & 0\\
0\\
\vdots & & \mathbf{I} - 2\hat{v_2}\hat{v_2}^T \\
0\\
\end{pmatrix}\\
\end{align}
We proceed in this fashion until all entries below the main diagonal are zero. Thus, \(\mathbf{Q}_n\mathbf{Q}_{n-1}\ldots\mathbf{Q}_1\mathbf{A}\) will be an upper triangular matrix.
We can now write out an algorithm for performing the QR decomposition using Householder transformations. This algorithm is rather straightforward but naive in the sense that a more efficient algorithm could be written.
input: A (m x n matrix)
output: Q (m x m matrix), R (m x n matrix)
u = m-dimensional vector
v = m-dimensional vector
I = identity matrix
P = I
Q = I
R = A
for i = 1 to n
u.zero()
v.zero()
for j = i to m
u[j] = R[j][i]
alpha = u[i] < 0 ? u.length() : -u.length()
for j = 1 to m
v[j] = j == i ? u[j] + alpha : u[j]
if (v.length() < epsilon) continue
v.normalize()
P = I - 2 * v * v.transpose()
R = P * R
Q = Q * P
end for
Below we have a C++ implementation of the decomposition algorithm above. The householderDecomposition method is a member of the cMatrix object. The cMatrix object is a rather simple object to perform a few matrix operations. It has a few operator overloads and the ability to transpose a matrix. Download the project at the end of this post to see the details. Here is the Householder decomposition.
void cMatrix::householderDecomposition(cMatrix& Q, cMatrix& R) {
double mag, alpha;
cMatrix u(m, 1), v(m, 1);
cMatrix P(m, m), I(m, m);
Q = cMatrix(m, m);
R = *this;
for (int i = 0; i < n; i++) { u.zero(); v.zero(); mag = 0.0; for (int j = i; j < m; j++) { u.A[j] = R.A[j * n + i]; mag += u.A[j] * u.A[j]; } mag = sqrt(mag); alpha = u.A[i] < 0 ? mag : -mag; mag = 0.0; for (int j = i; j < m; j++) { v.A[j] = j == i ? u.A[j] + alpha : u.A[j]; mag += v.A[j] * v.A[j]; } mag = sqrt(mag); if (mag < 0.0000000001) continue; for (int j = i; j < m; j++) v.A[j] /= mag; P = I - (v * v.transpose()) * 2.0; R = P * R; Q = Q * P; } } [/sourcecode] Download this project: qr_householder.cc.bz2